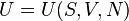miércoles, 9 de diciembre de 2015

maquina térmica y energía interna

En física, la energía interna (U) de un sistema intenta ser un reflejo de la energía a escala macroscópica. Más concretamente, es la suma de:

la energía cinética interna, es decir, de las sumas de las energías cinéticas de las individualidades que lo forman respecto al centro de masas del sistema,
la energía potencial interna, que es la energía potencial asociada a las interacciones entre estas individualidades.¹

La energía interna no incluye la energía cinética traslacional o rotacional del sistema como un todo. Tampoco incluye la energía potencial que el cuerpo pueda tener por su localización en un campo gravitacional o electrostático externo.

Todo cuerpo posee una energía acumulada en su interior equivalente a la energía cinética interna más la energía potencial interna.

Si pensamos en constituyentes atómicos o moleculares, será el resultado de la suma de la energía cinética de las moléculas o átomos que constituyen el sistema (de sus energías de traslación, rotación y vibración) y de la energía potencial intermolecular (debida a las fuerzas intermoleculares) e intramolecular de la energía de enlace.

En un gas ideal monoatómico bastará con considerar la energía cinética de traslación de sus átomos.
En un gas ideal poliatómico, deberemos considerar además la energía vibracional y rotacional de las mismas.
En un líquido o sólido deberemos añadir la energía potencial que representa las interacciones moleculares.

Desde el punto de vista de la termodinámica, en un sistema cerrado (o sea, de paredes impermeables), la variación total de energía interna es igual a la suma de las cantidades de energía comunicadas al sistema en forma de calor y de trabajo

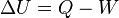\Delta U = Q - W

(En termodinámica se considera el trabajo negativo cuando este entra en el sistema termodinámico, positivo cuando sale). Aunque el calor transmitido depende del proceso en cuestión, la variación de energía interna es independiente del proceso, sólo depende del estado inicial y final, por lo que se dice que es una función de estado. Del mismo modo

dU

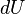es una diferencial exacta, a diferencia de

\eth Q

, que depende del proceso.

En termodinámica se deduce la existencia² de una ecuación de la forma

U=U(S,V,N) \qquad

conocida como ecuación fundamental en representación energética.

La importancia de la misma radica en que concentra en una sola ecuación toda la información termodinámica de un sistema. La obtención de resultados concretos a partir de la misma se convierte entonces en un proceso sistemático.

Si calculamos su diferencial:

dU=\left(\frac{\partial U}{\partial S}\right) dS +\left(\frac{\partial U}{\partial V}\right) dV +\left(\frac{\partial U}{\partial N}\right) dN

se definen sus derivadas parciales:

la temperatura $T = \frac{\partial U}{\partial S}$
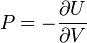
la presión $P = -\frac{\partial U}{\partial V}$
el potencial químico $\mu = \frac{\partial U}{\partial N}$ .

Como T, P y

\mu

son derivadas parciales de U, serán funciones de las mismas variables que U:

T=T(S,V,N) \qquad P=P(S,V,N) \qquad \mu=\mu(S,V,N)

Estas relaciones reciben el nombre de ecuaciones de estado. Por lo general no se dispone de la ecuación fundamental de un sistema. En ese caso sus sustitución por el conjunto de todas las ecuaciones de estado proporcionaría una información equivalente, aunque a menudo debamos conformarnos con un subconjunto de las mismas.

Al aumentar la temperatura de un sistema, sin que varíe nada más, aumenta su energía interna reflejado en el aumento de la energía térmica del sistema completo o de la materia estudiada.

Convencionalmente, cuando se produce una variación de la energía interna manifestada en la variación del calor que puede ser cedido, mantenido o absorbido se puede medir este cambio en la energía interna indirectamente por la variación de la temperatura de la materia.

Variación sin cambio de estado[editar]

Sin que se modifique el estado de la materia que compone el sistema, se habla de variación de la energía interna sensible o calor sensible y se puede calcular de acuerdo a los siguientes parámetros;

Q = C_e m \Delta T\!

Donde cada término con sus unidades en el Sistema Internacional son:

Q = es la variación de energía o de calor del sistema en un tiempo definido (J).

Ce = calor específico de la materia (J/kg·K).

m = masa.

\Delta T\!

= temperatura final del sistema - temperatura inicial (K).

Ejemplo[editar]

Calcular la energía total de un sistema compuesto de 1 g de agua en condiciones normales, es decir a la altura del mar, una atmósfera de presión y a 14 °C para llevarlo a 15º C, sabiendo que el Ce del agua es = 1 [cal/g·°C].

Aplicando la fórmula

Q = C_e m \Delta T\!

y reemplazando los valores, tenemos;

Q = 1 [cal/g·°C] · 1 [g] · (15 - 14) [°C] = 1 [cal]

Energía cinética media de un gas ideal[editar]

E_{cm} = \frac{3}{2} (K T) = \frac{1 }{2} m v_m^2\!

K = Constante de Boltzmann = 1,38·10^-23 J/K

v_m\!

=Velocidad media de la molécula

Las propiedades termodinámicas de un gas ideal pueden ser descritas por dos ecuaciones:

La ecuación de estado de un gas ideal clásico que es la ley de los gases ideales

PV = nRT\,

y la energía interna a volumen constante de un gas ideal que queda determinada por la expresión:

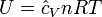
U = \hat{c}_V nRT

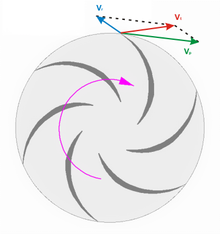
Máquina térmica

Máquina de vapor.

Motor Stirling.

Rotor de la turbina de vapor.

Rotores de un compresor de doble tornillo, un tipo de compresor volumétrico rotativo.

Un compresor de émbolos usado en un ciclo de refrigeración.

Compresor rotodinámico axial.

Compresor rotodinámico centrífugo y su triángulo de velocidades a la salida.

Una máquina térmica es un conjunto de elementos mecánicos que permite intercambiar energía, generalmente a través de un eje, mediante la variación de energía de un fluido que varía su densidad significativamente al atravesar la máquina. Se trata de una máquina de fluido en la que varía el volumen específico del fluido en tal magnitud que los efectos mecánicos y los efectos térmicos son interdependientes.

Por el contrario, en una máquina hidráulica, que es otro tipo de máquina de fluido, la variación de densidad es suficientemente pequeña como para poder desacoplar el análisis de los efectos mecánicos y el análisis de los efectos térmicos, llegando a despreciar los efectos térmicos en gran parte de los casos. Tal es el caso de una bomba hidráulica, a través de la cual pasa líquido. Alejándose de lo que indica la etimología de la palabra «hidráulica», también puede considerarse como máquina hidráulica un ventilador, pues, aunque el aire es un fluido compresible, la variación de volumen específico no es muy significativa con el propósito de que no se desprenda la capa límite.

En una máquina térmica, la compresibilidad del fluido no es despreciable y es necesario considerar su influencia en la transformación de energía.

Máquina térmica y motor térmico[editar]

En un principio se podría definir a una máquina térmica como un dispositivo, equipo o una instalación destinada a la producción de trabajo en virtud de un aporte calórico. Aunque en algunas definiciones se identifican como sinónimos los términos «máquina térmica motora» y «motor térmico», en otras se diferencian ambos conceptos. Al diferenciarlos, se considera que un motor térmico es un conjunto de elementos mecánicos que permite obtener energía mecánica a partir de la energía térmica obtenida mediante una reacciónde combustión o una reacción nuclear. Un motor térmico dispone de lo necesario para obtener energía térmica, mientras que una máquina térmica motora necesita energía térmica para funcionar, mediante un fluido que dispone de más energía a la entrada que a la salida.¹

Clasificación[editar]

Según el sentido de transferencia de energía[editar]

Las máquinas térmicas pueden clasificarse, según el sentido de transferencia de energía, en:

Máquinas térmicas motoras, en las cuales la energía del fluido disminuye al atravesar la máquina, obteniéndose energía mecánica en el eje.
Máquinas térmicas generadoras, en las cuales la energía del fluido aumenta al atravesar la máquina, precisándose energía mecánica en el eje.

Según el principio de funcionamiento[editar]

Atendiendo al principio de funcionamiento, las máquinas térmicas se clasifican en:

Máquinas volumétricas o máquinas de desplazamiento positivo, cuyo funcionamiento está basado en principios mecánicos ehidrostáticos, de manera que el fluido en algún instante está contenido en un volumen limitado por los elementos de la máquina. En este tipo de máquinas el flujo es pulsatorio. Se dividen a su vez en dos tipos según el movimiento del órgano propulsor: alternativas, cuyo movimiento es rectilíneo; y rotativas, cuyo movimiento es circular.
Turbomáquinas, cuyo funcionamiento está basado en el intercambio de cantidad de movimiento entre el fluido y un rodete. En estas máquinas el flujo es continuo.

Teniendo en cuenta lo anterior, podemos clasificar las máquinas térmicas tal como se recoge en el cuadro siguiente.

**Máquinas térmicas**
Motoras	Volumétricas	Alternativas	Máquina de vapor
		Rotativas	Motor Wankel
	Turbomáquinas		Turbina
Generadoras	Volumétricas	Alternativas	Compresor de émbolo
		Rotativas	Compresor rotativo
	Turbomáquinas		Turbocompresor

Balance de energía en una máquina térmica[editar]

Un sistema abierto es aquel que intercambia materia y energía con el entorno. Aplicando el primer principio de la termodinámica para unsistema abierto, el incremento de energía del sistema en un intervalo de tiempo es:

$\Delta E_{sistema} = Q + W + \sum_{in} m_{in} (h + \frac1 2 V^{2} + gz)_{in}-\sum_{out} m_{out} (h + \frac1 2 V^{2} + gz)_{out}$

donde;

Q es el calor entregado al sistema. Será negativo cuando el calor sea entregado por el sistema.
W es el trabajo entregado al sistema, en forma de trabajo mecánico y energía de presión. Será negativo cuando el calor sea entregado por el sistema.
El subíndice in representa la materia que entra al sistema.
El subíndice out representa la materia que sale del sistema.
h es la entalpía por unidad de masa del flujo
V²/2 es la energía cinética por unidad de masa del flujo.
gz es la energía potencial por unidad de masa del flujo

Haciendo la derivada de la expresión anterior respecto al tiempo, se obtiene: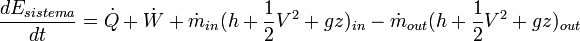

$\frac{dE_{sistema}}{dt} = \dot Q + \dot W + \dot m_{in} (h + \frac1 2 V^{2} + gz)_{in}- \dot m_{out} (h + \frac1 2 V^{2} + gz)_{out}$

Debe tenerse en cuenta que en máquinas generadoras, puede aparecer esta expresión con el signo de W cambiado, para que se exprese el trabajo entregado por la máquina y así W sea positivo.

Véase también: Criterio de signos termodinámico

Simplificaciones[editar]

La ecuación que expresa el balance de energía puede simplificarse en los siguientes casos:

Sistema en reposo

Cuando el sistema está en reposo, tal como en máquinas estacionarias, las variaciones de energía potencial y energía cinética serán nulas.

$\frac {dE_{sistema}}{dt} = \frac{dU}{dt} + \frac{E_c}{dt} + \frac{E_p}{dt} = \frac{dU}{dt}$
Régimen permanente

Cuando la máquina funciona en régimen permanente, las cantidades de masa y energía que entran son iguales a las que salen, pues de lo contrario variarían esa cantidades dentro del sistema.

$\dot m = \dot m_{in} = \dot m_{out}$; $\frac {dE_{sistema}}{dt} = 0$
Variación de energía potencial despreciable

En la mayoría de las máquinas térmicas, diferencia de energía potencial del flujo que sale respecto al que entra es poco significativo en comparación con los otros términos asociados a la energía del flujo.

$\Delta (gz) \ll \Delta \left (h + \frac1 2 V^{2} \right ) \Rightarrow \Delta (gz) \approx 0$
Sistemas adiabáticos

En la mayoría de las máquinas térmicas, la transferencia de calor es despreciable frente a otros intercambios de energía. Teniendo en cuenta la transmisión de calor porconducción y convección:

\dot Q = \frac{dQ}{dt} = U \cdot A \cdot \Delta T_{LM} \approx 0

donde Q es el calor intercambiado, U es el coeficiente global de transferencia de calor, A es la superficie del sistema y

\Delta T_{LM}

es la diferencia de temperaturas media logarítmica, puede considerarse que el sistema es adiabático cuando se da alguna de las siguientes condiciones:

La superficie externa del sistema está bien aislada térmicamente.
La superficie externa del sistema es muy pequeña.
La diferencia de temperaturas entre el flujo y el entorno del sistema es pequeña.
El fluido pasa a través de la máquina tan rápido que apenas hay tiempo para que sea significativa la transferencia de calor por unidad de masa.

Máquina térmica en régimen permanente con variación de energía potencial despreciable[editar]

En una máquina térmica que funciona en régimen permanente en la cual se desprecie la variación de energía potencial, la expresión el primer principio de la termodinámica puede expresarse como

$\dot W = \dot m [(h + \frac{V^{2}}{2})_{out} - (h + \frac{V^{2}}{2})_{in}] = \dot m [ h_{0 out} - h_{0 in} ]$

donde h₀ es la entalpía de parada.

En los ciclos termodinámicos asociados a la turbina de vapor, la energía cinética específica puede considerarse despreciable frente a la entalpía, resultando

$\dot W = \dot m [(h + \frac{V^{2}}{2})_{out} - (h + \frac{V^{2}}{2})_{in}] = \dot m [ h_{0 out} - h_{0 in} ]$

equilibrio térmico y cambios de estado

5:46 No comments

CAMBIOS DE ESTADO.

Paso de una sustancia de un estado a otro. Los más importantes son:

a) la evaporación

b) la condensación

c) la solidificación

d) la fusión

e) la vaporización

f) la sublimación

En un cambio de estado el cuerpo absorbe o desprende una determinada cantidad de calor por unidad de masa, denominado calor latente (de fusión, de ebullición, etc.), y durante el mismo la temperatura permanece invariable y constante para una presión externa dada.

Evaporación.

Paso de una sustancia del estado líquido al de vapor, a una temperatura inferior a la de ebullición. Tiene lugar sólo en la superficie del líquido y se produce de forma gradual.

Condensación.

Paso de una sustancia de la fase de vapor a la líquida (o la sólida); el proceso inverso es la vaporización (o la sublimación).

Solidificación.

Paso de un cuerpo del estado líquido al sólido; es el fenómeno inverso de la fusión. Para cada cuerpo tiene lugar a una temperatura determinada -punto de solidificación o de fusión- con desprendimiento de calor y, generalmente, acompañada de una disminución del volumen.

Fusión.

Paso de un cuerpo del estado sólido al líquido. Se verifica con absorción de calor, generalmente con aumento de volumen, y a una temperatura constante que depende de la naturaleza de los cuerpos y de la presión externa.

Vaporización.

Paso de una sustancia del estado líquido al gaseoso. Puede ser evaporación o ebullición según afecte sólo a la superficie o a todo el volumen. El calor de vapor es la cantidad de vapor que absorbe la unidad de masa de una sustancia al vaporizarse a una temperatura dada.

Sublimación.

Paso de un cuerpo directamente del estado sólido al de vapor o del de vapor al sólido; este último se llama también condensación. La transición sólido-vapor se produce cuando el sólido está sometido a una presión inferior a su presión de vapor, por lo que en muchos casos la cantidad de vapor en equilibrio con la fase sólida es mínima. Se llama calor de sublimación al absorbido (o desprendido) por la unidad de masa de una sustancia al sublimar.

Estado metastable.

El de un sólido, líquido o gas que permanece en un determinado estado de agregación en unas condiciones en que debería haberse producido un cambio de agregación.

La experiencia empírica indica que los cuerpos materiales adoptan diversas formas según el valor que toman las variables termodinámicas que los caracterizan.

El estado sólido se reconoce por la invariabilidad de forma y volumen; el estado líquido presenta sólo invariancia de volumen y el estado gaseoso carece de ambas. Para una misma sustancia y a presión constante, los estados sólido, líquido y gaseoso corresponden a valores crecientes de la temperatura. A temperaturas bajas, la energía cinética de las moléculas es insuficiente para superar las fuerzas de cohesión que tienden a mantenerlas unidas. Se tienen entonces los sólidos cristalinos. En éstos los movimientos de las moléculas se limitan a vibraciones en torno a determinados puntos que corresponden a los nudos de la red cristalina.

En el otro extremo del espectro, para valores muy superiores de la temperatura, la energía potencial intermolecular es prácticamente despreciable frente a la agitación molecular. El correspondiente estado de agregación es el gaseoso.

El estado intermedio corresponde a los líquidos y al estado amorfo: aunque pequeña, la velocidad de las moléculas es lo suficiente para que éstas no puedan formar un retículo cristalino.

Aumentando todavía la temperatura a partir del estado gaseoso, se llega a un punto en el que las moléculas se han disociado en sus átomos constituyentes y éstos a su vez han desaparecido para dar lugar a núcleos y electrones separados: este nuevo estado, característico de la materia estelar, se conoce con el nombre de plasma

El equilibrio térmico es aquel estado en el cual se igualan las temperaturas de dos cuerpos, las cuales, en sus condiciones iniciales presentaban diferentes temperaturas. Una vez que las temperaturas se equiparan se suspende el flujo de calor, llegando ambos cuerpos al mencionado equilibrio término.

El de equilibrio térmico es un concepto que forma parte de la termodinámica, la rama de la física que se ocupa de describir los estados de equilibrio a un nivel macroscópico.

Cuando dos sistemas se encuentran en contacto mecánico directo, o en su defecto, separados mediante una superficie que facilita la transferencia de calor, superficie diatérmica, se dirá que ambos están en contacto térmico. Mientras tanto, al cabo de un tiempo, aunque los dos sistemas que se hallan en contacto térmico se encuentren dispuestos de tal manera que no puedan mezclarse o aunque estén colocados en el interior de un espacio en el cual es imposible que intercambien calor con el exterior, indefectiblemente, alcanzarán el estado de equilibrio térmico.

A un nivel macroscópico, la situación de dos sistemas en contacto térmico podrá interpretarse porque las partículas de la superficie de interface de los dos sistemas son capaces de interactuar entre sí; lo que se verá es que las partículas del sistema que ostenta una mayor temperatura le transferirán parte de su energía a las partículas del otro sistema que observa una menor temperatura. La mencionada interacción hará que las partículas de ambos sistemas logren la misma energía y por tanto la misma temperatura.

Para poder conocer la temperatura que presenta un cuerpo o sustancia se emplea el dispositivo del termómetro. Cuando el termómetro entra en contacto térmico con el cuerpo en cuestión ambos alcanzarán el equilibrio térmico y entonces al encontrase en la misma temperatura, sabremos que la temperatura que nos indicará el termómetro en su índice será la temperatura del cuerpo que nos ocupa.

transferencia de calor por conducción y procesos termodinámicos.

5:43 No comments

Primera ley de la termodinámica.

La primera ley de la termodinámica establece que, cuando se añade calor Q a un sistema mientras éste efectúa trabajo W, la energía interna U cambia en una cantidad igual a Q – W.

La primera ley de termodinámica es la misma ley del principio de conservación de la energía, la cual exige que para todo sistema termodinámico se cumpla:

∆U = Q-W

Siendo ∆U la energía interna del sistema.

Trabajo en los gases.

Se considera un gas contenido en un cilindro provisto de un pistón, sobre el cual actúa la presión atmosférica P, cuando la temperatura del gas aumenta, el gas se expande a presión constante, cuando el gas se expande ejerce una fuerza F sobre el pistón y le produce un incremento en su volumen ∆V, de tal modo que el trabajo realizado por el gas sobre el pistón está dado por:

W = P*∆V

Procesos termodinámicos.

Proceso adiabático.

Se designa como proceso adiabático a aquel en el cual el sistema (generalmente, un fluido que realiza un trabajo) no intercambia calor con su entorno. Un proceso adiabático que es además reversible se conoce como proceso isentrópico.

El término adiabático hace referencia a elementos que impiden la transferencia de calor con el entorno. Una pared aislada se aproxima bastante a un límite adiabático. Otro ejemplo es la temperatura adiabática de una llama, que es la temperatura que podría alcanzar una llama si no hubiera pérdida de calor hacia el entorno. En climatización los procesos de humectación (aporte de vapor de agua) son adiabáticos, puesto que no hay transferencia de calor, a pesar de que se consiga variar la temperatura del aire y su humedad relativa.

Durante un proceso adiabático, la energía interna del fluido que realiza el trabajo debe necesariamente decrecer.

Es decir, que en este tipo de procesos se tiene que Q = 0. Que de acuerdo con la primera ley de la termodinámica, tenemos que:

Q= ∆U +W

Como Q =0, entonces, ∆U = -W.

Esto quiere decir, que para un gas contenido en un cilindro provisto de un pistón, cuyas paredes no permiten la transferencia de calor al exterior, la variación de energía interna es igual al trabajo, ya sea realizado por el sistema o sobre el sistema.

Proceso isotérmico.

En este proceso la temperatura permanece constante. Como la energía interna de una gas ideal sólo es función de la temperatura, en un proceso isotérmico de un gas ideal la variación de la energía interna es cero (∆U= 0) La curva hiperbólica se conoce como isotérmica.

De acuerdo con la primera ley de la termodinámica tenemos:

Q = ∆U +W.

Como ∆U = 0, entonces, Q = W

Este proceso se observa cuando en un pistón que contiene un gas, después de suministrarle calor y producir cambios tanto en la presión como en el volumen su temperatura permanece constante.

Proceso isobárico.

Es un proceso termodinámico en el cual la presión permanece constante, en este proceso, como la presión se mantiene constante, se produce una variación en el volumen y por tanto el sistema realiza trabajo o se puede realizar trabajo sobre el sistema.

De acuerdo con la primera ley de la termodinámica, tenemos:

Q = ∆U +W

Lo que quiere decir que en un proceso de tipo isobárico tanto el calor transferido como el trabajo realizado ocasionan una variación de la energía interna.

Proceso isométrico

En este proceso el volumen permanece constante, es decir que en este tipo de proceso el volumen no varía y por tanto el trabajo es igual a cero, lo que significa queW= 0.

De acuerdo con la primera ley de la termodinámica tenemos:

Q = ∆U +W

Como W=0, entonces Q = ∆U

Ejemplos.

1. Sobre un gas contenido en un cilindro provisto de un pistón se realiza un trabajo de 5000 J, mediante un proceso isotérmico. Determinar:

a. La variación de la energía interna del gas.

b. El calor absorbido o cedido por el gas.

Solución:

a. Puesto que el proceso es isotérmico, se tiene que ∆U = 0, luego la energía interna no varía.

b. Como el trabajo se realiza sobre el gas W = -5000 J, por tanto,

Q = ∆U + W

Q =0 – 5000J

Q = -5000J

Puesto que el calor es negativo, concluimos que el gas cede calor y su valor es 5000J.

2. En la figura, se muestra un diagrama P-V en el que se representan dos procesos A y B, a los que se somete un gas para pasar del estado 1 al estado 2. Determinar:

a. Las variables en los estados 2 y 3.

b. El proceso en el que se realiza mayor trabajo sobre el gas.

c. El proceso en el que es mayor el incremento de la energía interna.

d. El proceso en el que el sistema absorbe más calor.

T₂=400k

P₂

2 el proceso A es de tipo

P₃

Isotérmico, mientras que

el proceso B es adiabático.

T₁ =300k

P₁

V₂=2L

V₁=6L

Solución.

a. De las leyes de los gases

P₁V₁=P₂V₂ para temperatura constante y P₁V₁T₂= P₂V₂T₁ para temperaturas diferentes.

Luego en el proceso de los estados 1 a 3 como es un proceso isotérmico la temperatura es constante, así las variables del estado son:

P₁= 1 atm V₁=6L, V₃=2L, P₃=P₁V₁/ V₃ :P₃=1 atm*6L/2L=3atm, T₃=300k

Para el proceso de los estados 2 a 3, ocurre a volumen constante es decir, se presenta un proceso isométrico.

P₂V₂T₃= P₃V₃T₂ : P₂T₃= P₃T₂ : P₃=P₂T₃/T₂: P₃=3atm*400k/300K =4atm

Luego las variables de estado en el proceso 2 a 3 son:

P₃= 3 atm, P₂=4atm,

V=2L, T₃=300k, T₂=400k

b. Puesto que el área comprendida entre la gráfica y el eje horizontal es mayor para el proceso B, el trabajo realizado sobre el gas es mayor en dicho proceso. También observamos que en ambos procesos el gas se comprime lo que quiere decir que se realiza trabajo sobre el sistema.

c. Como en los dos procesos existe un cambio de temperatura de 100k, el incremento en la energía interna del sistema es igual en ambos casos.

d. El sistema no absorbe calor en el proceso B, puesto que se trata de un proceso adiabático, por tanto el gas absorbe más calor en el proceso A.

Taller de aplicación

El siguiente taller debe realizarse individualmente y hace parte del seguimiento (seguimiento 1) y deberá ser entregado en la próxima clase, con los cálculos respectivos y un análisis cualitativo de lo que se hace.

1. Tres moles de un gas ideal se llevan por el ciclo abc como muestra la figura, para este gas C_p= 29.1 J/mol*k. la temperatura del gas en los estados a, c y b es: T_a= 300k, T_c=492K y T_b=600k. determinar.

a. Los procesos termodinámicos que se presentan durante el ciclo, dibuje cada uno de ellos con diferente color y explique por qué se dan.

b. Los cambios de energía de cada proceso.

c. El trabajo total realizado por el ciclo.

d. El calor que absorbe o cede el sistema y haga una interpretación de este.

P1=1 atm

TRANSFERENCIA DE CALOR POR CONDUCCIÓN

La transmisión por conducción se produce cuando la energía se propaga debido a los choques entre las partículas.

En cada choque las partículas ceden parte de su energía cinética a las partículas contiguas, todo ello sin que haya transporte neto de materia.

En la animación anterior puedes ver cómo al encender la placa las patículas comienzan a moverse más rápidamente y la energía cinética se transmite desde las partículas de la placa vitrocerámica al cazo, a la parte metálica del mango y finalmente a la madera del mango, con el consiguiente aumento de temperatura en todas las zonas.

Este tipo de transmisión es característico de los sólidos, ya que los líquidos conducen muy mal y los gases prácticamente no conducen. Dentro de los sólidos existen muy buenos conductores del calor como los metales y malos conductores, como la madera o el papel.

Cuando dos partes de un material se mantienen a temperaturas diferentes, la energía se transfiere por colisiones moleculares de la mas alta a la mas baja temperatura. Este proceso de conducción es favorecido también por el movimiento de electrones libres en el interior de la sustancia, los cuales se han disociado de sus átomos de origen y tienen la libertad de moverse de uno a otro átomo cuando son estimulados ya sea térmica o eléctricamente. La mayoría de los metales son eficientes conductores del calor porque tienen cierto numero de electrones libres que pueden distribuir calor, además del que se propaga por la agitación molecular.

En general, un buen conductor de la electricidad también lo es del calor.“La ley fundamental de la conduccion térmica es una generalización de resultados experimentales relacionados con el flujo de calor a través de un material en forma de placa.”

1. La cantidad de calor transferido por unidad de tiempo es directamente proporcional a la diferencia de temperatura (Δt=t´ - t)

2. La cantidad de calor transferido por unidad de tiempo es inversamente proporcional al área A de la placa.

3. La cantidad de calor transferido por unidad de tiempo es inversamente proporcional al espesor de L de la placa.Estos resultados se pueden expresar en forma de ecuación introduciendo la constante de proporcionalidad K. Así pues escribimos nuestra primera formula:

H= Q/Τ=kA(Δt/L)
FORMULA 18.1

Donde:

H representa la razón con la que se transfiere el calor. Aun cuando la ecuación se estableció para un material en forma de placa, también se cumple para una barra de sección transversal A y longitud L.

La constante de proporcionalidad k es una propiedad de cada material que se conoce como conductividad térmica.

A partir de la ecuación anterior , se puede observar que las sustancias con alta conductividad térmica son buenas conductoras del calor, mientras que las sustancias con baja conductividad son conductoras pobres o aislantes.

“La conductividad térmica de una sustancia es una medida de su capacidad para conducir el calor y se define por medio de la relación:”

k= QL / ΤA Δt
FORMULA 18.2

FISICA

This is default featured slide 1 title

This is default featured slide 2 title

This is default featured slide 3 title

This is default featured slide 4 title

This is default featured slide 5 title

Recent Posts

Text Widget

Download